Welcome back to another exciting part of the n-body-problem post series. This time we are going to implement the Euler-Method to make the tests, we defined in the last post, pass. If you just dropped in or need to fresh up your memory see the links to the previous posts below. I also stumbled upon a very good presentation of the n-body-problem topic. Even if it's quite mathy, it serves us as good background information.

- My God, It’s Full Of Stars: The N-Body-Problem Series
- My God, It’s Full Of Stars: And then there was CMake
- My God, It’s Full Of Stars: Testing Point Mass Attraction with Catch2
In the last post we implemented two simple tests but while implementing the solver I realized we need clearly a bit more tests. Not only to test the solver, but we will need also some sort of Vector2D (later we might need a 3D variant) because we have to store and manipulate the position, velocity, and acceleration of a point mass. And all of these properties can be expressed as 2-dimensional vectors in a 2D space. To be useful Vector2D has to provide a couple of typical operations, such as addition, subtraction, multiplication and division with scalars. Additional we need to perform some negative tests for comparing a Vector2D. We would also need to test a division by zero case, which is asserted by operator/(), but as far as I found out Catch2 can't handle such cases at version 2.6.1 which we are using. This is how the test of Vector2D looks like.
TEST_CASE( "Test Vector2D operators and functions", "[vector]" ) {
const Vector2D vecA = { 1, 1 };
const Vector2D vecB = { 3, 3 };
SECTION( "Comparing vectors" ) {
const Vector2D expected = vecA;
REQUIRE(vecA == expected);
}
SECTION( "Length of a vector" ) {
REQUIRE(vecB.length() == Approx(sqrt(3*3 + 3*3)));
}
SECTION( "Adding two vectors" ) {
const Vector2D expected = { 4, 4 };
CHECK((vecA + vecB) == expected);
Vector2D result = vecA;
result += vecB;
REQUIRE(result == expected);
}
SECTION( "Subtracting two vectors" ) {
const Vector2D expected = { 2, 2 };
CHECK((vecB - vecA) == expected);
Vector2D result = vecB;
result -= vecA;
REQUIRE(result == expected);
}
SECTION( "Multiplying vector with scalar" ) {
const Vector2D expected = { 2, 2 };
CHECK((vecA * 2) == expected);
Vector2D result = vecA;
result *= 2;
REQUIRE(result == expected);
}
SECTION( "Dividing vector with scalar" ) {
const Vector2D expected = { 2, 2 };
CHECK((vecA * 2) == expected);
Vector2D result = vecA;
result *= 2;
REQUIRE(result == expected);
}
}
TEST_CASE( "Negative test Vector2D operators and functions", "[vector]" ) {
const Vector2D vecA = { 1, 1 };
SECTION( "Comparing vectors" ) {
Vector2D error = { 0, 1 };
CHECK_FALSE(vecA == error);
error = { 1, 0};
CHECK_FALSE(vecA == error);
error = { 0.999, 0.999 };
REQUIRE_FALSE(vecA == error);
}
SECTION( "Dividing vector with scalar" ) {
//Vector2D failing = vecA / 0;
//Catching asserts not possible with CATCH2 https://github.com/catchorg/Catch2/issues/853
}
}With the Vector2D class, we are fulfilling our tests and make them pass. The operator overloads are used to provide arithmetic operations between mathematical 2-dimensional vectors and scalars. Important to note is that the equality operator==() is comparing the absolute subtraction of both vectors. If they are equal, the result of the subtraction would be close to zero which is checked by comparing the result against std::numeric_limits<double>::min(). This utility template is representing the smallest possible finite value of a specific type and is part of the limits header. An alternative would be to check against relations of both values, but for the moment this would cause too many following issues, such as division by zero. Bruce Dawson is suggesting a comparison against an absolute epsilon based value, in case of comparisons against zero, which we are doing with the std::numeric_limits<double>::min().
struct Vector2D {
double x;
double y;
Vector2D() : x(0), y(0) {}
Vector2D(double x, double y) : x(x), y(y) {}
bool operator==(const Vector2D &rhs) const;
bool operator!=(const Vector2D &rhs) const;
double length() const;
Vector2D& operator-=(const Vector2D& rhs);
Vector2D& operator+=(const Vector2D& rhs);
Vector2D& operator*=(const double& rhs);
Vector2D& operator/=(const double& rhs);
};
Vector2D operator-(const Vector2D &lhs, const Vector2D &rhs);
Vector2D operator+(const Vector2D &lhs, const Vector2D &rhs);
Vector2D operator*(const Vector2D &lhs, const double &rhs);
Vector2D operator*(const double &lhs, const Vector2D &rhs);
Vector2D operator/(const Vector2D &lhs, const double &rhs);bool Vector2D::operator==(const Vector2D &rhs) const {
auto equalZero = std::numeric_limits<double>::min();
return fabs(x - rhs.x) <= equalZero &&
fabs(y - rhs.y) <= equalZero;
}
bool Vector2D::operator!=(const Vector2D &rhs) const {
return !(rhs == *this);
}
double Vector2D::length() const {
return sqrt(x*x + y*y);
}
Vector2D& Vector2D::operator-=(const Vector2D& rhs) {
*this = *this - rhs;
return *this;
}
Vector2D& Vector2D::operator*=(const double& rhs) {
*this = *this * rhs;
return *this;
}
Vector2D& Vector2D::operator/=(const double& rhs) {
*this = *this / rhs;
return *this;
}
Vector2D &Vector2D::operator+=(const Vector2D &rhs) {
*this = *this + rhs;
return *this;
}
Vector2D operator-(const Vector2D &lhs, const Vector2D &rhs) {
return { lhs.x - rhs.x,
lhs.y - rhs.y };
}
Vector2D operator+(const Vector2D &lhs, const Vector2D &rhs) {
return { lhs.x + rhs.x,
lhs.y + rhs.y };
}
Vector2D operator*(const Vector2D &lhs, const double &rhs) {
return { lhs.x * rhs,
lhs.y * rhs };
}
Vector2D operator*(const double &lhs, const Vector2D &rhs) {
return rhs * lhs;
}
Vector2D operator/(const Vector2D &lhs, const double &rhs) {
assert(fabs(rhs) > 0);
return { lhs.x / rhs,
lhs.y / rhs };
}We also need to extend the solver tests which are now running a couple of performance tests as well. We are doing this because we want to roughly determine how effective our algorithm is. Additional this gives us the ability to compare different algorithms against each other later on. And according to the paper of Christoph Schäfer, we expect a computational complexity around $O(N^2)$. Even if the PERFORMANCE clause is in a beta state, it works quite well.
double Inverse(double value) { return -value; }
Particle GenerateStandardParticle(double xPosition, double yPosition) {
ParticleBuilder particleBuilder;
return particleBuilder
.position({xPosition, yPosition})
.mass(1e10)
.build();
}
TEST_CASE( "Explicit euler algorithm with two point mass", "[euler]" ) {
const double EPSILON = 0.1;
Solver solver(EPSILON);
const std::vector<Particle> particlesX = { GenerateStandardParticle(0.5, 0),
GenerateStandardParticle(-0.5, 0)};
const std::vector<Particle> particlesY = { GenerateStandardParticle(0, 0.5),
GenerateStandardParticle(0, -0.5)};
//Solution
const double acceleration = -0.6674079993; //m/s^2
const double velocity = -0.06674079993; //m/s
const double position = 0.48665184; //m
SECTION( "Two still standing point mass are attracting each other in x-direction" ) {
std::vector<Particle> result = solver.solve(particlesX);
Particle &particle = result.front();
CHECK(particle.getAcceleration().x == Approx(acceleration));
CHECK(particle.getVelocity().x == Approx(velocity));
CHECK(particle.getPosition().x == Approx(position));
particle = result.back();
CHECK(particle.getAcceleration().x == Approx(Inverse(acceleration)));
CHECK(particle.getVelocity().x == Approx(Inverse(velocity)));
REQUIRE(particle.getPosition().x == Approx(Inverse(position)));
}
SECTION( "Two still standing point mass are attracting each other in y-direction" ) {
std::vector<Particle> result = solver.solve(particlesY);
Particle &particle = result.front();
CHECK(particle.getAcceleration().y == Approx(acceleration));
CHECK(particle.getVelocity().y == Approx(velocity));
CHECK(particle.getPosition().y == Approx(position));
particle = result.back();
CHECK(particle.getAcceleration().y == Approx(Inverse(acceleration)));
CHECK(particle.getVelocity().y == Approx(Inverse(velocity)));
REQUIRE(particle.getPosition().y == Approx(Inverse(position)));
}
}
TEST_CASE("Benchmarking euler", "[benchmark]") {
const double EPSILON = 0.1;
Solver solver(EPSILON);
ParticleBuilder particleBuilder;
std::vector<Particle> particles = particleBuilder.build(100);
BENCHMARK("Benchmarking with 100 particles") {
particles = solver.solve(particles);
}
particles = particleBuilder.build(200);
BENCHMARK("Benchmarking with 200 particles") {
particles = solver.solve(particles);
}
particles = particleBuilder.build(400);
BENCHMARK("Benchmarking with 400 particles") {
particles = solver.solve(particles);
}
particles = particleBuilder.build(800);
BENCHMARK("Benchmarking with 800 particles") {
particles = solver.solve(particles);
}
particles = particleBuilder.build(1600);
BENCHMARK("Benchmarking with 1.6K particles") {
particles = solver.solve(particles);
}
particles = particleBuilder.build(3200);
BENCHMARK("Benchmarking with 3.2K particles") {
particles = solver.solve(particles);
}
particles = particleBuilder.build(6400);
BENCHMARK("Benchmarking with 6.4K particles") {
particles = solver.solve(particles);
}
particles = particleBuilder.build(12800);
BENCHMARK("Benchmarking with 12.8K particles") {
particles = solver.solve(particles);
}
particles = particleBuilder.build(25600);
BENCHMARK("Benchmarking with 25.6K particles") {
particles = solver.solve(particles);
}
}Because we will need to generate a random number of point masses we also introduced a simple ParticleBuilder utility class, based on an adapted and simplified builder pattern with a fluent interface, which can generate single particles or any arbitrary number of particles needed. In our case, we use this to generate our benchmark particles. The basic principle of the builder pattern is that each method, which is configuring a specific property of a point mass, is returning a reference to itself. This way we can concatenate all (or only some if necessary) methods together and build at the end the point mass. The actual generation of the point mass is done at the very end of the definition process which is called lazy initialization. To generate the random values of the point mass properties we take, as suggested by Vorbrodt's article about random number generators, the std::random_device, which we use as a random seed of the std::mersenne_twister_engine::mt19937 to produce the actual random number we need. The range of the random numbers will be uniformly distributed between 1 and the number of point masses to generate.
class ParticleBuilder {
public:
ParticleBuilder() : mMass(0) {}
ParticleBuilder & position(const Vector2D &position);
ParticleBuilder & velocity(const Vector2D &velocity);
ParticleBuilder & acceleration(const Vector2D &acceleration);
ParticleBuilder & mass(double mass);
Particle build() const;
std::vector<Particle> build(size_t numberOfParticles);
private:
double mMass;
Vector2D mAcceleration;
Vector2D mVelocity;
Vector2D mPosition;
};ParticleBuilder & ParticleBuilder::position(const Vector2D &position)
{
mPosition = position;
return *this;
}
ParticleBuilder & ParticleBuilder::velocity(const Vector2D &velocity)
{
mVelocity = velocity;
return *this;
}
ParticleBuilder & ParticleBuilder::acceleration(const Vector2D &acceleration)
{
mAcceleration = acceleration;
return *this;
}
ParticleBuilder & ParticleBuilder::mass(double mass)
{
mMass = mass;
return *this;
}
Particle ParticleBuilder::build() const
{
return {mMass, mAcceleration, mVelocity, mPosition};
}
std::vector<Particle> ParticleBuilder::build(size_t numberOfParticles)
{
std::vector<Particle> particle(numberOfParticles);
std::mt19937 mt(std::random_device{}());
std::uniform_real_distribution real_dist(1.0, static_cast<double>(numberOfParticles));
for(Particle &p : particle) {
p = mass(real_dist(mt))
.acceleration({ real_dist(mt), real_dist(mt) })
.velocity({ real_dist(mt), real_dist(mt) })
.position({ real_dist(mt), real_dist(mt) })
.build();
}
return particle;
}The Particle class is then basically straight forward. The only important topic that we have to somehow define is how are we determine if two particles are actually the same. This can't be done by simply comparing their reference, because we never altering the particles them self, but producing new ones after each operation. All particles are handled as immutable. Because of this, we need to somehow assign a unique ID to every point mass which we are doing by simply assigning a class IDCounter onto the id member and incrementing IDCounter afterward.
class Particle {
public:
Particle();
Particle(double mass, const Vector2D &acceleration, const Vector2D &velocity, const Vector2D &position);
bool operator==(const Particle &rhs) const;
bool operator!=(const Particle &rhs) const;
double getMass() const;
const Vector2D &getAcceleration() const;
void setAcceleration(const Vector2D &acceleration);
const Vector2D &getVelocity() const;
void setVelocity(const Vector2D &velocity);
const Vector2D &getPosition() const;
void setPosition(const Vector2D &position);
private:
static size_t IDCounter;
size_t id;
double mass;
Vector2D acceleration;
Vector2D velocity;
Vector2D position;
};size_t Particle::IDCounter = 0;
Particle::Particle()
: mass(0) {
id = IDCounter++;
}
Particle::Particle(double mass, const Vector2D &acceleration, const Vector2D &velocity, const Vector2D &position)
: mass(mass), acceleration(acceleration), velocity(velocity), position(position) {
assert(mass > 0);
id = IDCounter++;
}
bool Particle::operator==(const Particle &rhs) const {
return id == rhs.id;
}
bool Particle::operator!=(const Particle &rhs) const {
return !(rhs == *this);
}
const Vector2D &Particle::getAcceleration() const {
return acceleration;
}
void Particle::setAcceleration(const Vector2D &acceleration) {
Particle::acceleration = acceleration;
}
const Vector2D &Particle::getVelocity() const {
return velocity;
}
void Particle::setVelocity(const Vector2D &velocity) {
Particle::velocity = velocity;
}
const Vector2D &Particle::getPosition() const {
return position;
}
void Particle::setPosition(const Vector2D &position) {
Particle::position = position;
}
double Particle::getMass() const {
return mass;
}Last but not least we have the actual implementation of the Euler-Method. The Solver class gets initialized by the necessary time step $\epsilon$ and has only one simple interface method which takes a std::vector<Particle> as parameter and returns, after computation is done, the result. In order to execute its computation, the solve method is using the methods calculateAcceleration, calculateVelocity, and calculatePosition, which basically all have the same interface. The essence of the computation, the calculation of the acceleration of a point mass by the gravitational force of all the other point masses, is then done inside the static function AccumulateAcceleration. You might realize that we strongly focused on using functionality provided by the STL, there is even no real for loop. This is done that way because I had the idea of using the execution policy's of the STL, later on, but then realized that this is not supported until now by libc++ (P0024R2).
class Solver {
public:
explicit Solver(double mEpsilon);
std::vector<Particle> solve(const std::vector<Particle> &particles) const;
private:
std::vector<Particle> calculateAcceleration(const std::vector<Particle> &particles) const;
std::vector<Particle> calculateVelocity(const std::vector<Particle> &particles) const;
std::vector<Particle> calculatePosition(const std::vector<Particle> &particles) const;
static Particle AccumulateAcceleration(const std::vector<Particle> &particles, const Particle &particle);
static double CalculateEquivalentMass(const Particle &particleA, const Particle &particleB);
static const double G;
static const double EPSILON;
double mEpsilon;
};const double Solver::G = 6.67408e-11;
const double Solver::EPSILON = 1e-3;
Solver::Solver(double mEpsilon) : mEpsilon(mEpsilon) {}
std::vector<Particle> Solver::solve(const std::vector<Particle> &particles) const {
std::vector<Particle> solution = calculateAcceleration(particles);
solution = calculateVelocity(solution);
solution = calculatePosition(solution);
return solution;
}
std::vector<Particle> Solver::calculateAcceleration(const std::vector<Particle> &particles) const {
std::vector<Particle> solution(particles.size());
std::transform(begin(particles), end(particles), begin(solution), [&particles](const Particle &particle) {
return AccumulateAcceleration(particles, particle);
});
return solution;
}
std::vector<Particle> Solver::calculateVelocity(const std::vector<Particle> &particles) const {
std::vector<Particle> solution(particles.size());
std::transform(begin(particles), end(particles), begin(solution), [epsilon = mEpsilon](Particle particle) {
const Vector2D v0 = particle.getVelocity();
particle.setVelocity(v0 + particle.getAcceleration()*epsilon);
return particle;
});
return solution;
}
std::vector<Particle> Solver::calculatePosition(const std::vector<Particle> &particles) const {
std::vector<Particle> solution(particles.size());
std::transform(begin(particles), end(particles), begin(solution), [epsilon = mEpsilon](Particle particle) {
const Vector2D v = particle.getVelocity();
const Vector2D r0 = particle.getPosition();
particle.setPosition(r0 + v*epsilon + particle.getAcceleration()*epsilon*epsilon);
return particle;
});
return solution;
}
Particle Solver::AccumulateAcceleration(const std::vector<Particle> &particles, const Particle &particle) {
Particle particleA = particle;
const double e3 = EPSILON*EPSILON*EPSILON;
std::for_each(begin(particles), end(particles), [&particleA, e3](const Particle &particleB) {
if(particleA != particleB) {
const double M = CalculateEquivalentMass(particleA, particleB);
const Vector2D r = particleB.getPosition() - particleA.getPosition();
const double rLength = r.length();
const double r3 = fabs(rLength*rLength*rLength);
const Vector2D a0 = particleA.getAcceleration();
particleA.setAcceleration(a0 + G*M*r/(r3 + e3));
}
});
return particleA;
}
double Solver::CalculateEquivalentMass(const Particle &particleA, const Particle &particleB) {
const double massA = particleA.getMass();
assert(massA > 0);
const double massB = particleB.getMass();
return massA*massB/massA;
}We accomplished quite a bit up to this point. We got now a simple but working algorithm which is computing us a solution for a discrete time step of the n-body-problem. But how does our first draft perform? First of all, all tests are passing, great. And we are even able to calculate with a reasonable number of point masses. But we have to remind our selves that we need for only one time step with 25.6K point masses around 45 seconds. That's quite a lot. If we just see the numbers we might realize that the statement of the computational complexity of the Euler-Method is $O(N^2)$, the diagram below shows it even more drastic. And it's totally true. If we would exchange the std::transform, of the calculateAcceleration method, and the std::for_each algorithm, of the AccumulateAcceleration function, with simple for loops, we would easily realize that we have a nested for loop of N point masses. The rest is then just math, $N \cdot N=N^2$.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
solverTest is a Catch v2.6.1 host application.
Run with -? for options
-------------------------------------------------------------------------------
Benchmarking euler
-------------------------------------------------------------------------------
/mnt/c/Develop/gravity/solverTest/src/solverTest.cpp:63
...............................................................................
benchmark name iters elapsed ns average
-------------------------------------------------------------------------------
Benchmarking with 100 particles 1 532000 532 µs
Benchmarking with 200 particles 1 3663900 3.6639 ms
Benchmarking with 400 particles 1 12501000 12.501 ms
Benchmarking with 800 particles 1 49732100 49.7321 ms
Benchmarking with 1.6K particles 1 182535600 182.536 ms
Benchmarking with 3.2K particles 1 711535000 711.535 ms
Benchmarking with 6.4K particles 1 2612469200 2.61247 s
Benchmarking with 12.8K particles 1 11103358400 11.1034 s
Benchmarking with 25.6K particles 1 46714864800 46.7149 s
===============================================================================
All tests passed (25 assertions in 4 test cases)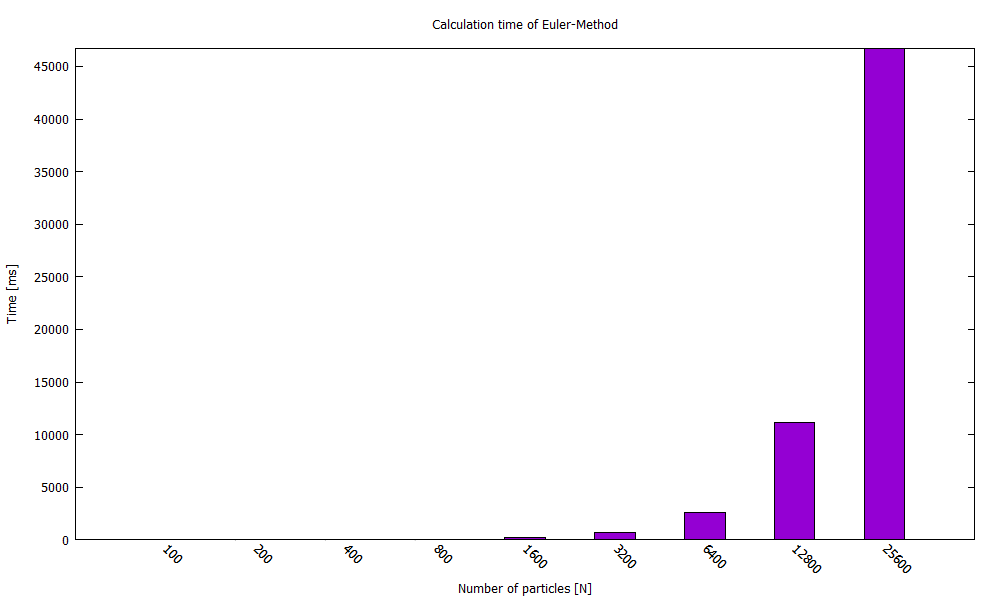
Till this point, we focused only on readability as much as possible, and I think we could even more. But I would like to focus on two certain issues on the next post, the efficiency of the algorithm and parallelization. If you would like to download the project at this state, feel free to get v0.4.0.
Since you've made it this far, sharing this article on your favorite social media network and giving feedback would be highly appreciated 💖!
Published