I thought it would be a very nice idea to start my blog with a small project I wanted to do since a long time. A small tool/solver of the n-body-problem. It's not just only the interest of solving a challenging mathematical problem with modern C++. I also love clean, concise and readable code, which is also something I would like to train and share with this project. You can find the empty repository setup at GitHub. I will always try to tag the end state of the repository after each post of this blog series.

So lets start with the bare minimum of theory we need. We want to start with a simple example of two still standing masses (or stars if you like) which get attracted to each other. For the sake of simplicity we consider them as point masses which mean they are infinitesimal small, or in other words, they have no volume.
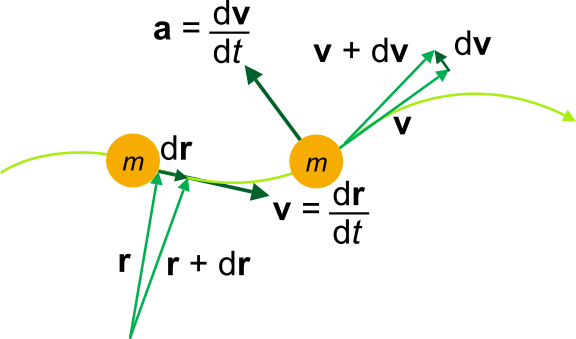
Kinematic quantities of a classical particle of mass m: position r, velocity v, acceleration a (Wikipedia)
From the image above we can see that a particle is moving the path $dr$, with its velocity $v$ and accelerated by $a$. From this point we get the equations of motion of one such point as
$$r=r_{0}+vt+\frac{1}{2}at^{2}$$
with $r$ as the resulting position, $r_{0}$ as the starting position, $v$ as the velocity, $t$ as the time step and $a$ as the acceleration. We also know that the force is defined by the product of mass $m$ and the acceleration $a$
$$F=ma$$
We know as well that the force due to gravity between two masses can be calculated as
$$F=G\frac{m_{1}m_{2}}{r^2}$$
with the gravitational constant $G$ the two masses of them and their distance $r$. With the equations of the force and the force due to gravity, we can derive the acceleration $a$ a mass point is experiencing while he is attracted by another mass point.
$$a=G\frac{m_{1}m_{2}}{m_{1}r^2}$$
As a result we get our final equation which is deriving the change of position of a mass point by its starting position, its velocity and its acceleration.
$$r=r_{0}+vt+\frac{1}{2}G\frac{m_{1}m_{2}}{m_{1}r^2}t^{2}$$
With this I will close this post and we will proceed next time with setting up a basic CMAKE example project which is building our solver library and a separate test library.
Since you've made it this far, sharing this article on your favorite social media network and giving feedback would be highly appreciated 💖!
Published